Composite Functions – An Ultimate Guides On How To Solve Composite Functions With 5 Examples
Table of Contents
In mathematics, a function can be defined as a principle that establishes a connection between a specific group of inputs and a corresponding range of potential outputs. It is essential to emphasize that each input within a function is uniquely associated with a single output.
The act of assigning names to functions is referred to as function notation. Common symbols used in function notation include “f(x) = …,” “g(x) = …,” “h(x) = …,” and so on.
This text aims to provide instruction on composite functions and their solution methods.
What is a Composite Function?
A composite function is typically a function that is embedded within another function. The process of composing a function involves substituting one function with another.
Given two functions, creating a new function by combining them through composition is possible. The steps involved in this process resemble those used to solve any function for a given value. These functions are commonly referred to as composite functions.
For instance, f [g (x)] represents the composite function of f (x) and g (x). The notation f [g (x)] is read as “f of g of x.” The function g (x) is called the inner function, while the function f (x) is called the outer function. Consequently, f [g (x)] can also be interpreted as “the function g is the inner function of the outer function f.”
How to Solve Composite Functions?
To indicate the composition of a function, we utilize a small circle symbol (∘). Below are the steps outlining how to solve a composite function.
For example
(f ∘ g) (x) = f [g (x)]
(f ∘ g) (x) = f [g (x)]
(f ∘ g) (x²) = f [g (x²)]
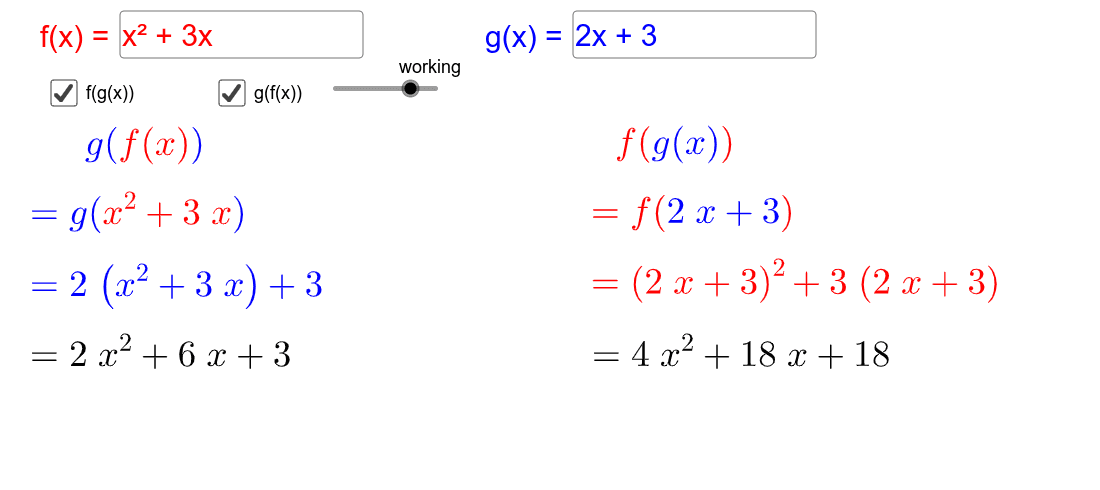
The first step is to replace the variable x in the outer function with the inner function. Afterward, simplify the resulting function.
The sequence or order of functions in the composition is significant because (f ∘ g) (x) is not equivalent to (g ∘ f) (x).
Examples of Problem Solved
example 1
Given the functions f (x) = x2 + 4 and g (x) = 2x – 1, find (f ∘ g) (x).
solving
Substitute x with 2x – 1 in the function f(x) = x2 + 4
(f ∘ g) (x) = (2x – 1)2 + 4 = (2x – 1) (2x – 1) + 4
Apply FOIL
= 4x2 – 4x + 1 + 4
= 4x2 – 4x + 5
Example 2
Given f (x) = 2x + 2, find (f ∘ f) (x).
Solution
(f ∘ f) (x) = f[f(x)]
= 2(2x + 2) + 2
= 4x + 4
Example 3
Find (g ∘ f) (x) given that, f (x) = 2x + 3 and g (x) = –x2 + 5
Solving
⟹ (g ∘ f) (x) = g [f (x)]
Replace x in g(x) = –x2 + 5 with 2x + 3
= – (2x + 3)2 + 5
= – (4x2 + 12x + 9) + 5
= –4x2 – 12x – 9 + 5
= –4x2 – 12x – 4
Example 4
Find (g ∘ f) (x) if, f(x) = 6 x² and g(x) = 14x + 4
Solving
⟹ (g ∘ f) (x) = g [f(x)]
Substitute x in g(x) = 14x + 4 with 6 x²
⟹g [f(x)] =14 (6 x²) + 4
= 84 x² + 4
Example 5
Calculate (f ∘ g) (x) using f(x) = 2x + 3 and g(x) = -x 2 + 1,
Solving
(f ∘ g) (x) = f(g(x))
= 2 (g(x)) + 3
= 2(-x 2 + 1) + 3
= – 2 x 2 + 5
